ngram “smoothing”

Recap

In the notes on information theory, we talked about how we can evaluate texts with respect to language models, and vice versa, with metrics like perplexity.

But we run into trouble with really novel sentences, when the probability is estimated to be 0. This can happen for one of two reasons:

Where 0 probabilities come from

“Out of Vocabulary Items”

“Out of Vocabulary Items” or OOVs are tokens that were not present in the training data. This won’t be so common for closed-vocabulary tokenizers, like Byte Pair Encoding, but for tokenization like we’ve used on Moby Dick, this is guaranteed to happen.

python

"ogre" in moby_dick_tokens

False

OOVs aren’t just the domain of ngram models, but also come up in, say, looking up word pronunciations in pronunciation dictionaries.

True

[nltk_data] Downloading package cmudict to
[nltk_data]     /Users/joseffruehwald/nltk_data...
[nltk_data]   Package cmudict is already up-to-date!

python

from nltk.corpus import cmudict
cmu_dictionary = cmudict.dict()

python

cmu_dictionary["philadelphia"]

[['F', 'IH2', 'L', 'AH0', 'D', 'EH1', 'L', 'F', 'IY0', 'AH0']]

python

cmu_dictionary["passyunk"]

KeyError: 'passyunk'

Missing Sequences

Even if every token is represented in the training data, specific sequences aren’t.

python

"screamed" in moby_dick_tokens

True

python

scream_idx = moby_dick_tokens.index("screamed")
moby_dick_tokens[
  (scream_idx-3):(scream_idx+3)
]

['Wa-hee', '!', '”', 'screamed', 'the', 'Gay-Header']

A predictable problem

An interesting thing is that there is a pretty good way to estimate whether the next token you see in a corpus will be new to you. It’s approximately equal to the probability that you’ll see a token that’s only appeared once so far.

\[ P(\text{new}) \approx P(\text{once)} \]

It takes a lot of processing to actually calculate, but here’s how the Good-Turing estimate works out for the book Frankenstein.

Good Turing Smoothing

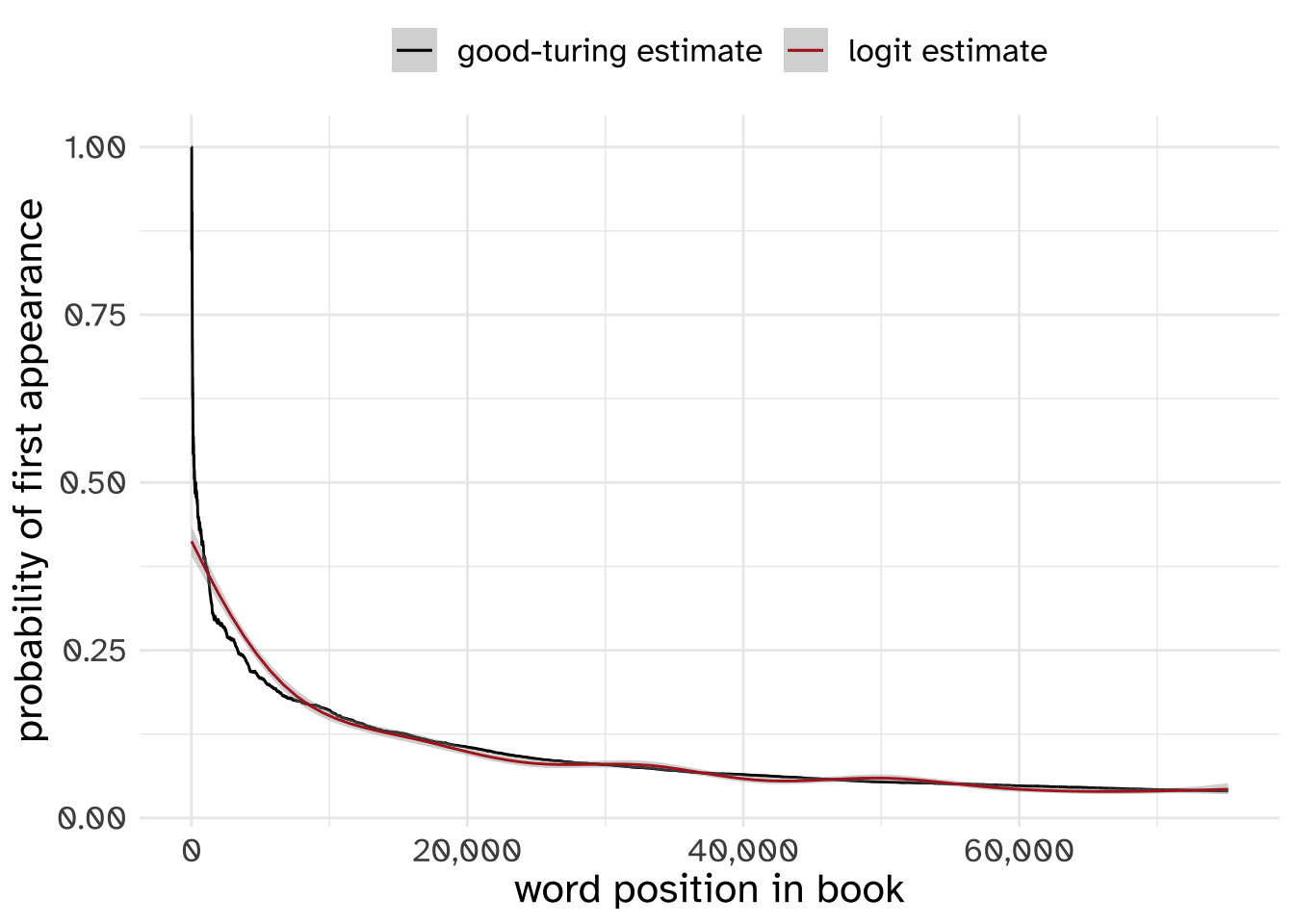
So, for Moby Dick, we can calculate the probability that a new token will be completely new.

python

counter_dict = Counter(moby_dick_words)
ones = 0
for k in counter_dict:
  if counter_dict[k] == 1:
    ones+=1
    
ones / counter_dict.total()

0.04445651239656506

Maybe that doesn’t seem so bad, but remember, the problem only gets worse the larger our ngrams get.

The proportion of all tokens which are hapax legomena

Dealing with it

Unkifying

One thing you can do to deal with the OOV issue is convert all tokens below a certain frequency to the label <UNK> for “unknown.”

python

moby_count = Counter(moby_dick_tokens)
moby_unk_tokens = moby_dick_tokens
for idx, tok in enumerate(moby_unk_tokens):
  if moby_count[tok] < 2:
    moby_unk_tokens[idx] = "<UNK>"

moby_unk_count = Counter(moby_unk_tokens)

python

check_word  = "ogre"
if check_word in moby_unk_count:
  print(moby_unk_count[check_word])
else:
  print(moby_unk_count["<UNK>"])

11379

NLTK conveniently. builds this into is vocabulary module.

python

from nltk.lm import Vocabulary
moby_vocab = Vocabulary(moby_dick_tokens, unk_cutoff = 2)

python

moby_vocab.lookup("ogre")

'<UNK>'

Smoothing

Even after unkifying, there are still going to be some ngrams where the individual tokens occur in the training data, but the specific sequence doesn’t.

So, we estimated the probability that the next token we see is going to be new token:

python

ones / counter_dict.total()

0.04445651239656506

The problem is, in order to give unseen token a slice of the pie, we need to take away some space from the seen tokens. Where does that probability fit into this layer cake, where all the space is already accounted for?