Sampling from a probability distribution

From an n-gram model, we can generate new sequences by sampling from the probability distribution over tokens.

From counts to proportions

Let’s start by saying we’re working with a bigram model (counts of 2 token sequences). If we start with an input token “the”, how do we randomly generate the next token?

Let’s restrict our view to just the top 5 words that followed “the” in Moby Dick:

Frequency of words that come after ‘the’

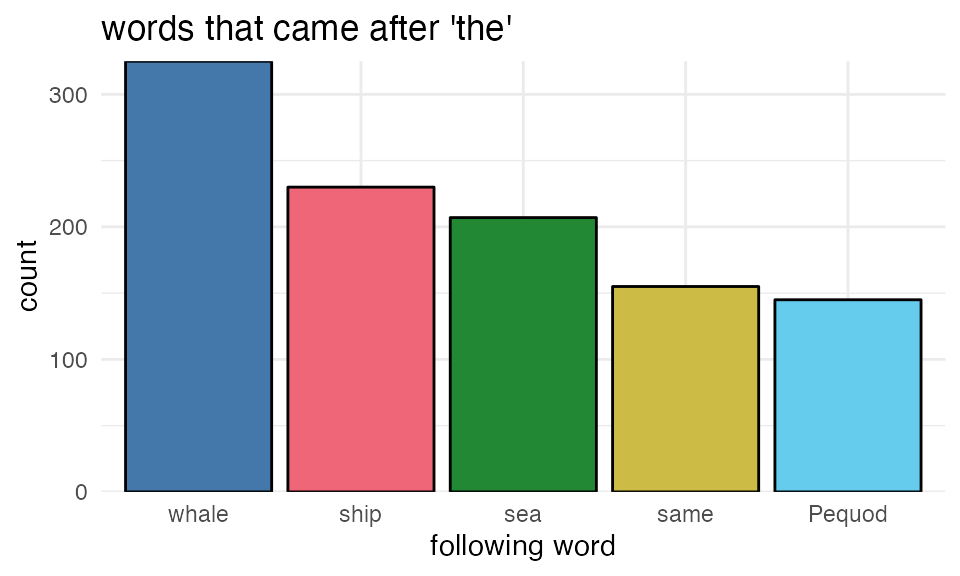
We can re-express these frequencies as proportions by dividing each frequency by the sum of all frequencies.

\[ P(w_i|w_{i-1}) = \frac{C(w_{i-1}w_i)}{\sum(w_{i-1}w)} \]

Proportion of words that come after ‘the’

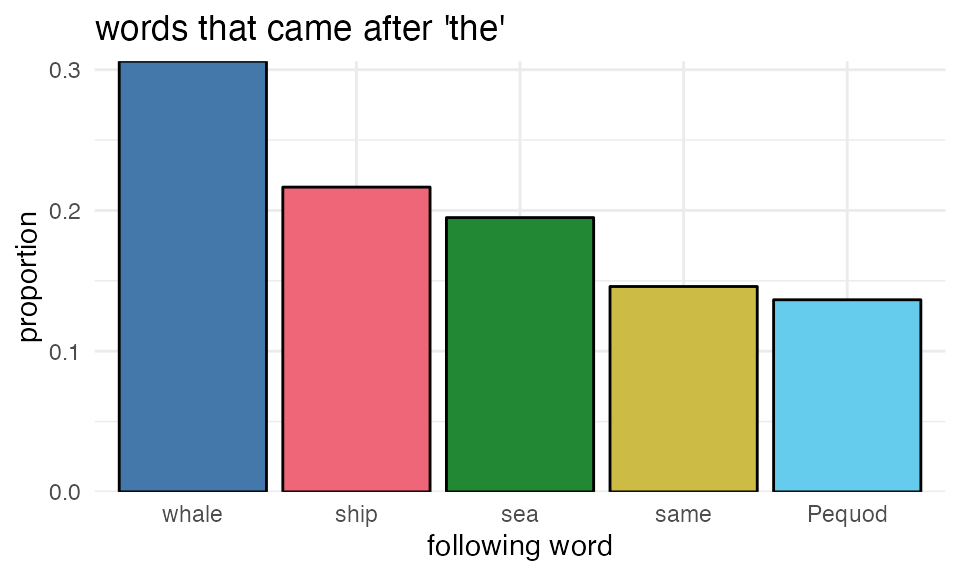
These two plots should look the same, just with different labels on the y-axis.

From proportions to a “probability distribution”

Now, if we stack each bar on top of each other and lie it flat, we get the “probability distribution” over tokens. The rectangle for each word represents how much probability it “takes up”.

Words as a probability distribution

Sampling from the probability distribution

To sample from this probability distribution, we can randomly throw darts at the figure above. Whichever rectangle the dart lands inside, we’ll say is the word we “sampled”.

Just be super clear that the 20 ❌es in the next plot are totally at random, I’ll include the code that I used to generate them.

r

tibble(
  samp = runif(20, min = 0, max = 1)
) ->
  rand_samples

Random samples from a probability distribution

If we count up the total number of ❌es in each square above, the order of highest to lowest frequency samples probably won’t perfectly line up with the tokens that had the highest to lowest probabilities.

fol	n
whale	8
sea	5
same	4
ship	2
Pequod	1

A little more realistic

If we try to get just a little bit more realistic, and look at the top 100 tokens that follow “the”, we’ll see that a single randomly sampled token is very often not going to be the highest probability token.

Randomly sampling from the top 100

fol	n	prop
most	110	0.02

Different Probability distributions

Words occur at different frequencies in different contexts, so they’ll have different probability distributions in each context. Even the same “dart throws will return different sampled words if the probability distributions are different.

	"The _"		"the _"
	n	proportion	n	proportion
whale	12	0.26	325	0.31
ship	13	0.28	230	0.22
sea	2	0.04	207	0.19
same	4	0.09	155	0.15
Pequod	15	0.33	145	0.14

	"The _"	"the _"
whale	7	8
ship	3	2
sea	1	5
same	2	4
Pequod	7	1